Using a Hashmap

Preamble

We, as programmers, want our algorithms to run as fast and as memory efficient as possible. This however, is hard. When do we know that we’ve hit the right solution? And how do we even measure that? In this post I’m trying to explain how to do exactly that.

The problem

Suppose we have an array: [2, 7, 11, 15]. We want to find the indices of two numbers that add up to our target. So lets say our target is 9. We want to fetch the two indices of the numbers that add up to 9, which would be 2 and 7, and get their indices, which would be [0, 1].

Note that the array can be unsorted.

The (naive) solution

The first solution everyone thinks about is to just iterate through the array twice. A little bit like this (rust code ahead):

let mut solution: Vec<i32> = Vec::new();

for (i_index, i) in nums.iter().enumerate() {
    for (x_index, x) in nums.iter().enumerate() {
        if x_index == i_index {
            continue;
        }
        
        if i + x == target {
            solution.push(i_index as i32);
            solution.push(x_index as i32);
            
            return solution;
        }
    }
}    

solution

Big O notation

I hope it is apparent to you why this is not an optimal solution. When both numbers that add up to the target are at the end, we have virtually traversed the list twice. This isn’t really a problem with modern hardware when the lists are small, but when the list are big (maybe thousands, maybe millions of elements), the computation time exponentially grows.

We can measure the complexity of our algorithm with Big O(n) notation. Big O tells you the number of operation it takes to complete your algorithm, not how long it will take in seconds. The less the better. A Big O of 1 is best. No matter the size of the list, it will always take 1 operation to complete your algorithm. Think of something like a switch statement, where it is always known where the compiler should jump to.

Next best is a Big O(log n). The number of operations increase with a log of n. Think of a binary search algorithm.

Big O(n) is the most average case. Think of getting finding an element in an unsorted array.

Big O(n * log n) is slow. Think of a divide and conquer algorithm.

A Big O(n^2) is quite frankly, bad. Think of running a nested for loop, as we did above.

Big O(n!) is the worst. Think of BogoSort.

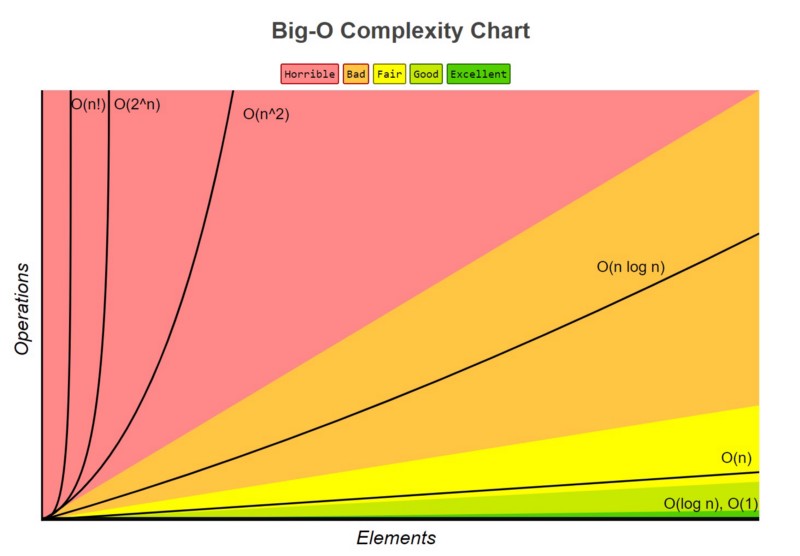
Source: FreeCodeCamp

The (less naive) better solution

So last solution had a Big O(n^2), can we do better?

Matter of fact, we can. I gave a clue in the preamble. The hint is that the array is unsorted. So if we sort the array, then we can binary search for the number we need. This yields us a Big O(n * log n)

The algorithm I came up with works as follows:

1. Sort the array.
2. Iterate through the list.
3. Compute the number we need: (target - current_element).
4. Does it exist? return the index of the current element and the element you’ve found.
5. It does not exist? Try again with the next element.

Hashmap

A Big O(n * log n) is decent, but not optimal. Can we do even better?

What if we had some sort of a list, that can hold all of the integers we’ve already iterated through? We can’t really use a regular array for that, because the find function still takes O(n), so that won’t really help us. Is there something else we can use?

There is! and it’s called a Hashmap.

With a regular array, it takes about O(n) to find an element. This is because you basically have to traverse the whole array (worst-case) to find the element you are looking for.

Storing values in a Hashmap works in a different way. The indices aren’t sequential, like in a traditional array, but the indices are calculated using a hash function. It works like this:

To store a value:

calculate hash of element -> store element at that hash

To retrieve a value:

calculate hash of the element you want to find -> use it as an index

This ensures the look-up time is O(1) on average.

A solution in linear time

So the algorithm I came up with to solve this problem in linear time goes as follows:

1. Create a HashMap and put the index of the first element in and use the first element as the hash.
2. Go through the rest of the list.
3. Compute the number that you’re looking for.
4. Check if that number exists in the HashMap.
5. It does? Take the index of the current number and that number and return it.
6. It doesn’t? Put the index of the element in the HashMap with the element as the hash.
7. Repeat.

let mut solution: Vec<i32> = Vec::new();
let mut key_store = HashMap::new();

for (i, x) in nums.iter().enumerate() {
    if i == 0 {
        key_store.insert(x, i);
        continue;
    }
    
    let intermediate: i32 = target - x;
    
    match key_store.get(&intermediate) {
        Some(s) => {
            solution.push(s.to_owned() as i32);
            solution.push(i as i32);
        },
        None => {
            key_store.insert(x, i);
            continue;
        }
    }
}        

solution